IT/모바일
복권 시뮬레이션
시뮬레이션의 개념을 이해하기 위해 베르누이 분포를 따르는 확률변수를 시뮬레이션으로 생성하는 방법을 설명합니다. 또한 컴퓨터로 생성되는 확률변수를 난수라고 부를 수 있습니다.
이 책에서는 확률변수와 난수라는 용어를 거의 같은 의미로 사용합니다. 앞으로 소개하는 방법은 베르누이 분포를 따르는 난수를 생성하는 시뮬레이션이라고 할 수 있습니다.
컴퓨터에서 가상으로 추첨을 수행해볼 것입니다. 당첨이 2장, 꽝이 8장 들어간 검은 상자에서 무작위로 복권을 1장 뽑습니다. 그리고 복권이 당첨인지 여부를 기록합니다. 무작위로 추첨하므로 0.2 확률로 당첨이 나온다고 가정합니다.
따라서 이 추첨 시뮬레이션은 성공확률 베르누이 시행으로 생각할 수 있습니다
분석 준비
필요한 라이브러리를 불러옵니다.
| In | # 수치 계산에 사용하는 라이브러리 import numpy as np import pandas as pd from scipy import stats
# 그래프를 그리는 라이브러리 from matplotlib import pyplot as plt import seaborn as sns sns.set()
# 그래프의 한글 표기 from matplotlib import rcParams rcParams['font.family'] = "Malgun Gothic" |
복권 1장 시뮬레이션
복권을 1장 뽑는 시뮬레이션을 실행합니다. 간단하지만 파이썬으로 시뮬레이션하는 방법은 다른 분야에도 응용할 수 있으니 꼭 익혀두기 바랍니다.
넘파이 배열로10장짜리 복권 변수lottery를 준비합니다. 숫자1이 당첨이고 0이 꽝입니다.
| In | lottery = np.array([1,1,0,0,0,0,0,0,0,0]) lottery |
| Out | array([1, 1, 0, 0, 0, 0, 0, 0, 0, 0]) |
당첨 수를 전체 복권의 매수로 나누어 성공확률을 구할 수 있습니다. 이번에는10장 중2장이 당첨이므로 성공확률은 0.2입니다.
| In | sum(lottery) / len(lottery) |
| Out | 0.2 |
이제 복권을 1장 뽑습니다. 넘파이 배열에서 모든 요소를 동일한 확률로 추출하려면 다음과 같이 np.random.choice 함수를 사용합니다. 함수의 인수로 추출할 대상이 되는 복권 lottery와 복권을 뽑는 횟수인 size를 지정합니다. replace=True는 한 번 뽑은 복권을 다시 상자로 되돌리는 인수 지정입니다. 이를 복원추출이라고 합니다. 뽑은 복권을 되돌리지 않으면 비복원추출이라고 합니다. 이번에는 복권을1장만 뽑으므로 설정할 필요는 없지만 참고하기 위해서 설정해둡니다.
| In | np.random.choice(lottery, size=1, replace=True) |
| Out | array([0]) |
결과는 넘파이 배열입니다. 이번에는 꽝 복권이 나왔습니다. 복권을 한 번 뽑는 시도를 세 번 반복해봅시다
| In | print(np.random.choice(lottery, size=1, replace=True)) print(np.random.choice(lottery, size=1, replace=True)) print(np.random.choice(lottery, size=1, replace=True)) |
| Out | [0] [1] [0] |
첫 번째와 세 번째는 꽝이었지만 두 번째는 당첨입니다. 같은 코드를 실행하고 있지만 실행할 때마다 확률적으로 결과가 바뀝니다. 여러분이 앞의 코드를 실행하면 첫 번째 시도에서 당첨이 나오거나 세 번 다 꽝이거나 등 실행할 때마다 다른 결과가 나타날 것입니다. 이처럼 파이썬 시뮬레이션을 활용하면 확률적 변동을 이해하는 데 매우 유용합니다.
복권 10장 시뮬레이션
다음으로 베르누이 시행을 넘어 10장의 복권 뽑기 결과를 확인하는 시뮬레이션을 실행합니다. 성공확률이 0.2인 복권을 10장 뽑았을 때 모두 꽝인 확률이나 1장만 당첨이 나올 확률은 얼마일까요. 이는 나중에 소개할 이항분포라는 확률분포에 해당합니다.
우선 복권을 10장 뽑는 방법을 설명합니다. np.random.choice 함수의 인수에 size=10이라고 설정하기만 하면 복권을 10장 뽑을 수 있습니다.
| In | print(np.random.choice(lottery, size=10, replace=True)) print(np.random.choice(lottery, size=10, replace=True)) print(np.random.choice(lottery, size=10, replace=True)) |
| Out | [0 0 0 0 0 0 0 0 0 0] [0 0 0 0 1 0 0 0 0 0] [0 0 0 0 0 1 0 0 1 0] |
세 번 실행했지만 결과는 무작위로 바뀝니다. 첫 번째는 10장 모두가 꽝이었습니다. 두 번째는 당첨이 1장, 세 번째는 당첨이 2장입니다.
난수 생성 시뮬레이션은 확률적으로 결과가 바뀝니다. 그러나 난수 시드random seed를 지정하여 결과를 고정할 수 있습니다. 이 책에 기재한 내용과 같은 결과를 여러분이 재현할 수 있도록 여기에서 난수 시드를 소개합니다.
난수 시드를 설정하려면 np.random.seed 함수를 사용합니다. 인수에는 원하는 숫자를 넣습니다. 같은 숫자를 지정하면 같은 결과가 나옵니다. 이번에는 인수에1을 설정했습니다.
| In | np.random.seed(1) print(np.random.choice(lottery, size=10, replace=True)) np.random.seed(1) print(np.random.choice(lottery, size=10, replace=True)) np.random.seed(1) print(np.random.choice(lottery, size=10, replace=True)) |
| Out | [0 0 0 0 1 1 1 0 0 0] [0 0 0 0 1 1 1 0 0 0] [0 0 0 0 1 1 1 0 0 0] |
np.random.seed 함수와 np.random.choice 함수를 번갈아 실행하면 확실히 3장의 당첨이 나옵니다. 앞의 코드를 여러 번 실행해도 마찬가지입니다.
np.random.seed 함수를 한 번 실행한 후 np.random.choice 함수를 연속으로 실행하면 결과는 무작위로 바뀝니다.
| In | np.random.seed(1) print(np.random.choice(lottery, size=10, replace=True)) print(np.random.choice(lottery, size=10, replace=True)) print(np.random.choice(lottery, size=10, replace=True)) |
| Out | [0 0 0 0 1 1 1 0 0 0] [0 0 0 0 0 0 0 0 0 0] [1 0 1 0 0 0 0 0 0 1] |
첫 번째는 당첨 3장, 두 번째는 당첨 0장, 세 번째는 당첨 3장입니다. 이러한 변화의 패턴은 난수시드를 지정하는 것으로 고정됩니다. 즉 앞의 코드를 다시 실행해도 ‘첫 번째는 당첨 3장, 두 번째는 당첨 0장, 세 번째는 당첨 3장’이 되는 것은 변하지 않습니다.
| In | np.random.seed(1) print(np.random.choice(lottery, size=10, replace=True)) print(np.random.choice(lottery, size=10, replace=True)) print(np.random.choice(lottery, size=10, replace=True)) |
| Out | [0 0 0 0 1 1 1 0 0 0] [0 0 0 0 0 0 0 0 0 0] [1 0 1 0 0 0 0 0 0 1] |
np.sum 함수를 사용하면 추첨 결과를 합산하여 당첨 매수를 알 수 있습니다.
| In | np.random.seed(1) sample_1 = np.random.choice(lottery, size=10, replace=True) print('당첨 결과:', sample_1) print('당첨 매수:', np.sum(sample_1)) |
| Out | 당첨 결과: [0 0 0 0 1 1 1 0 0 0] 당첨 매수: 3 |
복권 10장 시행을 1만 회 반복하는 시뮬레이션
복권을 10장 뽑고 당첨 매수를 기록하는 시행을 1만 회 반복 실행해봅시다. 우선 시뮬레이션을준비합니다. 시행횟수인 n_trial을10000으로 설정했습니다. 또한1만 회의 결과를 저장하기위해binomial_result_array를 준비했습니다.
| In | # 시행횟수 n_trial = 10000 # 결과물을 담을 변수 binomial_result_array = np.zeros(n_trial) |
이어서 시뮬레이션을 시행합니다. 첫 번째 줄에서 난수 시드를 설정합니다. 두 번째 줄은 for반복문입니다. 인덱스 i를 0에서 n_trial까지 늘리면서 아래 두 줄의 코드를 반복해서 실행합니다.
for 문에서 np.random.choice 함수를 사용하여 복권을 뽑아 결과를 sample에 저장합니다. size=10으로 지정하여 복권은 10장 뽑습니다. 그리고 당첨 수를 binomial_result_array에 저장합니다.
| In | np.random.seed(1) for i in range(0, n_trial): sample = np.random.choice(lottery, size=10, replace=True) binomial_result_array[i] = np.sum(sample) |
binomial_result_array의 처음 10개를 가져옵니다. 당첨이 3장 나오거나, 1장 나오거나, 전혀 나오지 않는 등, 무작위로 결과가 바뀌고 있는 것을 알 수 있습니다.
| In | binomial_result_array[0:10] |
| Out | array([3., 0., 3., 2., 3., 1., 0., 2., 3., 0.]) |
이제 시뮬레이션 결과의 상대도수분포를 얻습니다. 계급은 0에서 10까지1씩 변화시켰습니다.
| In | np.histogram(binomial_result_array, bins=np.arange(0, 11, 1), density=True) |
| Out | (array([1.118e-01, 2.711e-01, 2.992e-01, 1.977e-01, 8.890e-02, 2.430e-02, 5.800e-03, 1.100e-03, 1.000e-04, 0.000e+00]), array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])) |
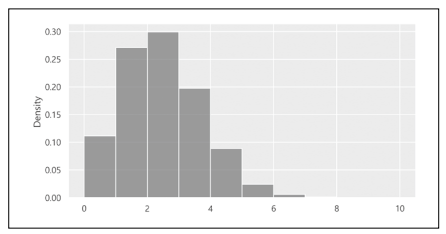
이어서 히스토그램을 그립니다. 예상할 수 있듯이 당첨 매수가 2장인 부근에 사람이 많은 것을 알 수 있습니다.
| In | sns.histplot(binomial_result_array, bins=np.arange(0, 11, 1)) stat='density', color='gray') |

파이썬 코드로 풀어보는 친절한 통계학 입문서
콘텐츠 추천, 데이터 분석 등 현대 사회의 중요한 의사결정은 통계를 기반으로 이루어집니다. 하지만 통계학의 수식과 이론만으로는 그 개념이 잘 와닿지 않을 때가 많습니다. 이 책은 그러한 어려움을 덜어주고자 이론과 더불어 파이썬 코드와 실습을 통해 직관적으로 이해할 수 있는 길을 안내합니다. 넘파이와 팬더스 라이브러리로 데이터를 분석하고, 맷플롯립과 시본을 이용해 데이터를 시각화합니다.
기술통계, 확률과 분포, 통계적 추정, 가설검정 등 통계의 기본을 다지고 나아가 머신러닝과의 접점까지 살펴봅니다. 이론에만 머무르지 않고 실제 데이터를 분석하며 통계 이론을 익히는 방식은 통계를 학습하는 데 큰 도움이 될 것입니다. 통계가 어렵게만 느껴졌다면 이 책으로 시작해보세요.
이전 글 : 챗GPT만 활용해서 탄핵소추안 작성하기
최신 콘텐츠
